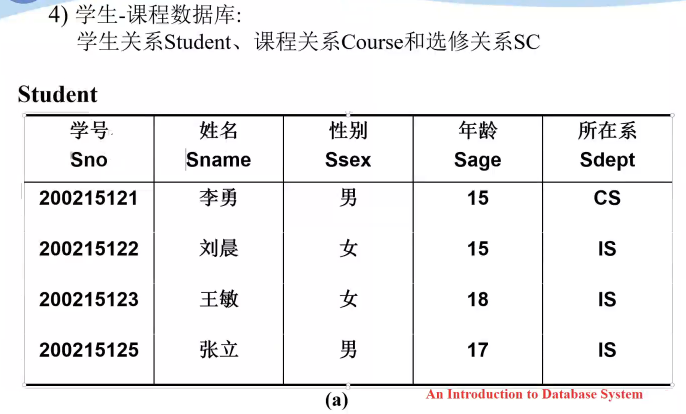
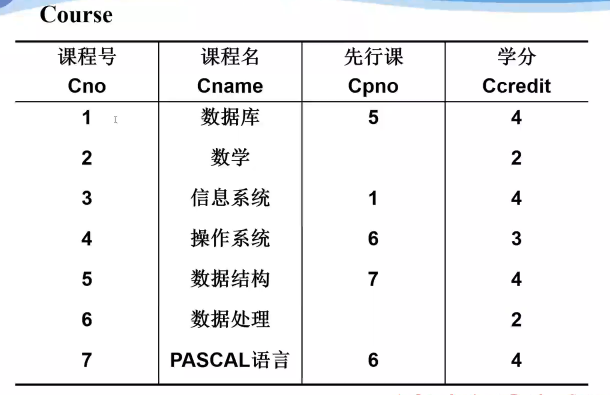
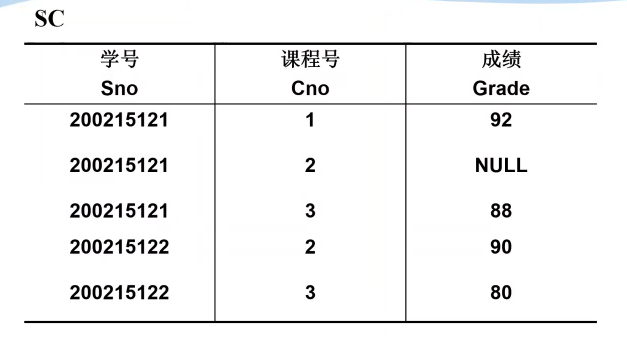
二、关系数据库
域、投影操作、选择操作、链接操作、自然连接、左右连接
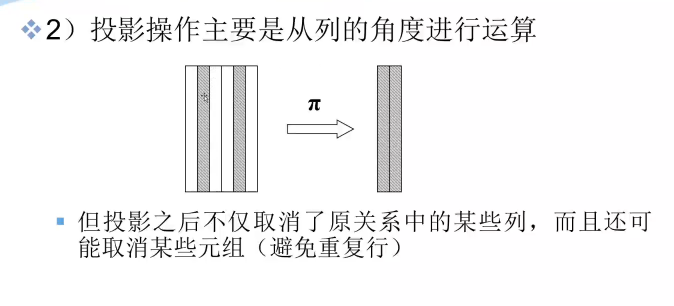
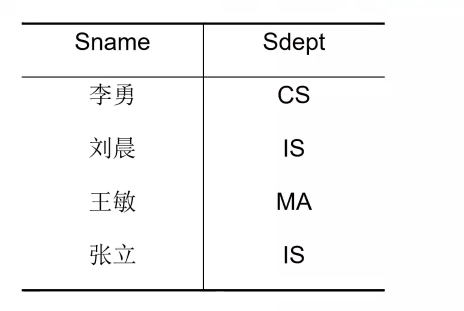
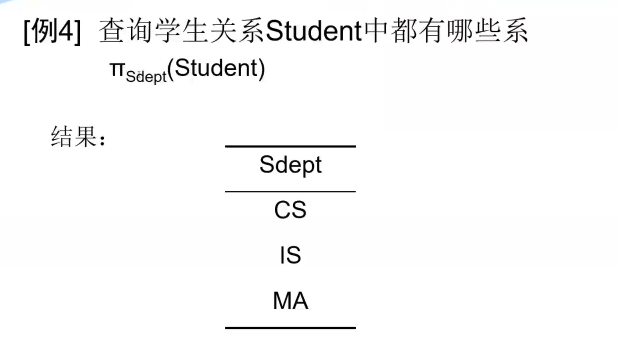
在关系代数的专门运算中,从表中取出指定的属性(列)的操作称为:投影
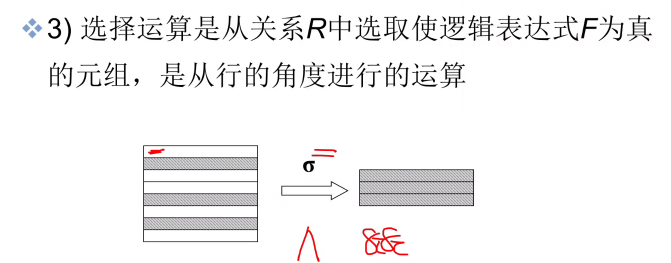
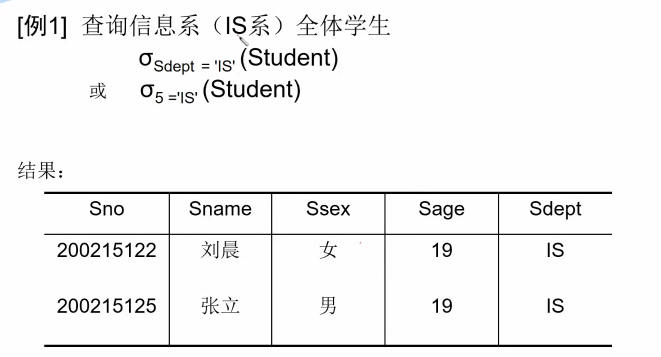
从表中选出满足某种条件的元组操作称为:选择
提出关系模型的是美国IBM公司的E.F.Codd
1970年提出关系数据模型
E.F.Codd,”A Relational Model of Data for Large Shared Data Banks”,《Communication of the ACM》,1970
之后,提出了关系代数和关系演算的概念
1972年提出了关系的第一、第二、第三范式
1974年提出了关系的BC范式
2.1、关系数据结构及形式化定义
1、关系
单一的数据结构——关系
现实世界的实体以及实体间的各种联系均用关系来表示
逻辑结构——二维表
从用户角度,关系模型中数据的逻辑结构是一张二维表
建立在集合代数的基础上
域(domain)
域是一组具有相同数据类型的值的集合。比如:整数、实数、介于某个取值范围的整数,长度指定长度的字符串集合
笛卡尔积(Cartesian Product)
给定一组域D1,D2,。。。,Dn,这些域中可以有相同的
D1,D2,。。。,Dn的笛卡尔积为:
D1×D2×…×Dn={(d1,d2,…,dn)|di∈Di,i = 1, 2, .., n}
所有域的所有取值的一个组合
不能重复基数(Cardinal number)
笛卡尔积的表示方法
- 笛卡尔积可表示为一个二维表
- 表中的每行对应一个元组,表中的每列对应一个域
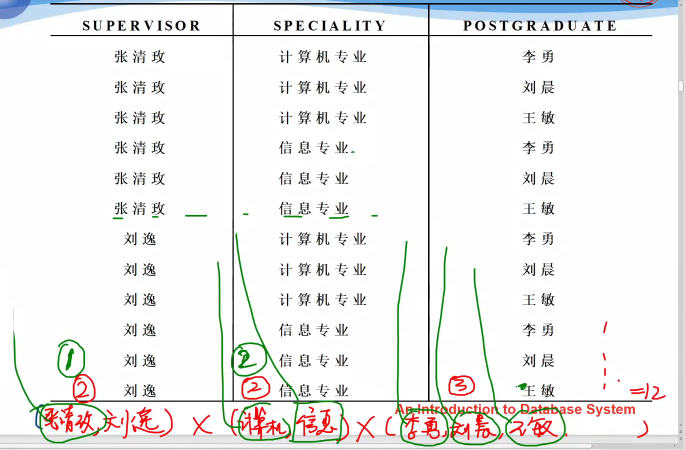
元组(Tuple)
关系中的每个元素都是关系中的元组,用t表示。
笛卡尔积中每一个元素(d1, d2, …, dn)叫做一个n元组(n-tuple)或简称元组(Tuple)
(张庆梅,计算机专业,李勇)是元组
分量(Component)
- 笛卡尔积元素(d1, d2, …, dn)中的每一个di 都叫做一个分量
- 张庆梅、计算机专业、李勇、都是分量
关系(Relation)
D1×D2×。。。×Dn的子集叫做在域D1,D2,。。。Dn上的关系,表示为
R(D1, D2, …, Dn)
R:关系名
n:关系的目或度(Degree)单元关系与二元关系
- 当n=1时,称该关系为单元关系或一元关系
- 当n=2时,称该关系为二元关系
关系的表示
- 关系是一个二维表,表的每行对应一个元组,表的每列对应一个域
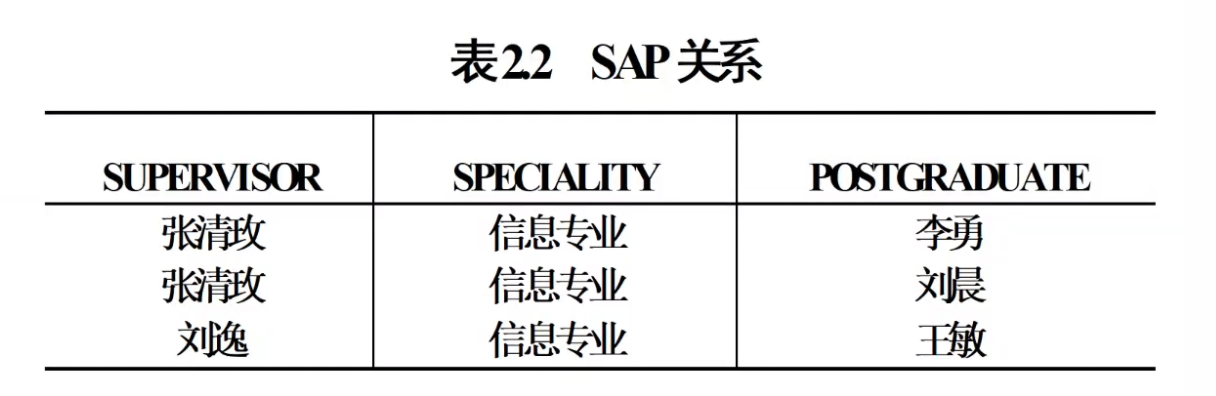
属性(attribute)
- 关系中不同列可以对应相同的域
- 为了加以区分,必须对每列起一个名字,成为属性
- n目关系必有n个属性
码(key)
候选码(Candidate key)
- 若关系中的某一属性组的值能惟一地标识一个元组,则称该属性组为候选码
- 简单的情况:候选码只包含一个属性
- 候选码中的属性称为:主属性
全码(All-key)
- 最极端的情况:关系模式的所有属性组是这个关系模式的候选码,称为全码(All-key)
主码
- 若一个关系有多个候选码,则选定其中一个为主码(Primary key)
主属性
- 候选码的诸属性成为主属性(Prime attribute)
- 不包含在任何候选码中的属性称为非主属性(Non-Prime attribute)或非码属性(Non-key attribute)

三类关系
基本关系(基本表或基表)
- 实际存在的表,是实际存储的逻辑表示
查询表
- 查询结果对应的表
视图表
- 由基本表或其他视图表导出的表,是虚表,不对应实际存储的数据
基本关系的性质
列是同质的(Homogeneoous)
不同的列可出自同一个域
- 其中的每一列称为一个属性
- 不同的属性要给予不同的属性名
列的顺序无所谓,列的次序可以任意交换
任意两个元组的候选码不能相同
行的顺序无所谓,行的次序可以任意交换
分量必须取原子值
- 这是规范条件中最基本的一条
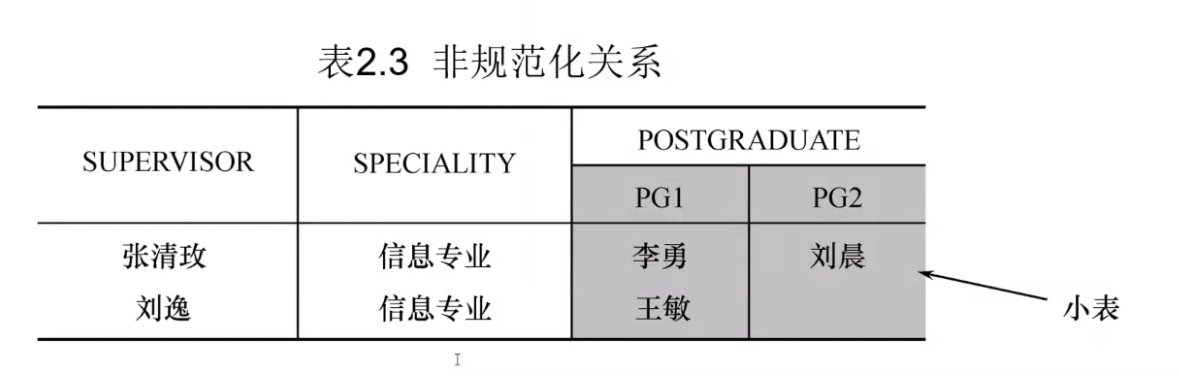
2、关系模式



2.2、关系操作
2.3、关系的完整性
2.4、关系代数
关系代数用关系的运算表示查询,主要分为两类集合
运算和专门的关系运算
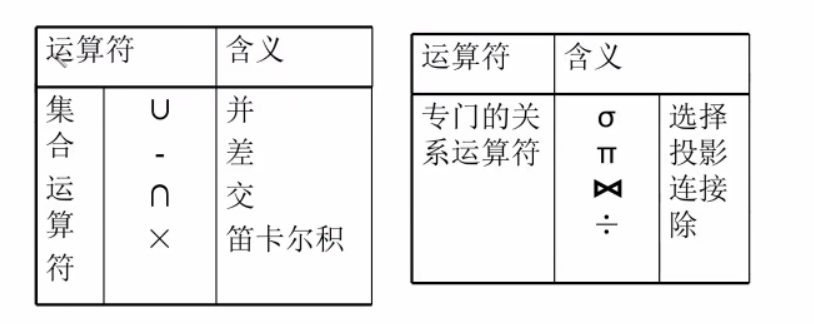
1、并(Union)
R和S
- 具有相同的目n(即两个关系都有n个属性)
- 相应的属性取自同一个域
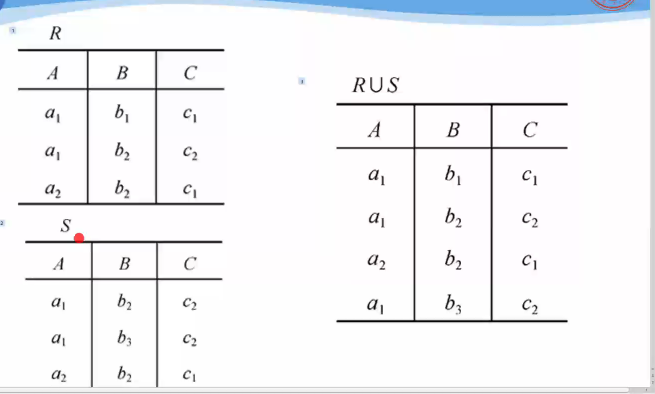
R∪S
- 仍为n目关系,由属于R或属于S的元组组成
R∪S={t | t∈R V t∈S}
2、差(Difference)
R和S
- 具有相同的目n(即两个关系都有n个属性)
- 相应的属性取自同一个域
R - S
- 仍为n目关系,由属于R而不属于S的元组组成
R - S={t | t∈R ∧t∉ S}

3、交(Intersection)
R和S
- 具有相同的目n(即两个关系都有n个属性)
- 相应的属性取自同一个域
R ∩ S
仍为n目关系,由属于R又属于S的元组组成
R ∩ S={t | t∈R ∧t∈ S}R ∩ S = R - (R - S)
4、笛卡尔积(Cartesian Product)
严格地讲应该是广义的笛卡尔积(Extended Cartesian Product)
R:n目关系,k1个元组
S:n目关系,k2个元组
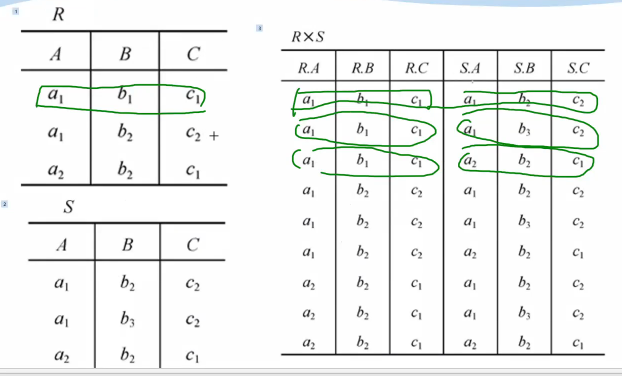
R×S
- 列:(n+m)列元组的集合
- 元组的前n列是关系R的一个元组
- 后m列是关系S的一个元组
- 行:k1×k2个元组
- R×S = {trts | tr∈ R ∧ ts∈S}
5、专门的关系运算
(1)R,t∈R, t[Ai]
设关系模式为R(A1, A2, …, An)
它的一个关系设为R
t∈ R表示 t 是R 的一个元组
t[Ai]则表示元组 t 中相应于属性 Ai的一个分量
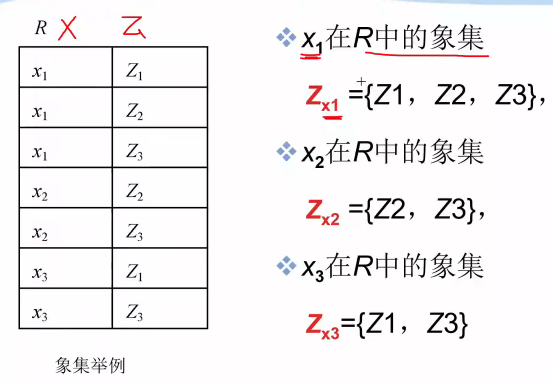
(2)A, t[A], $\overline{A}$



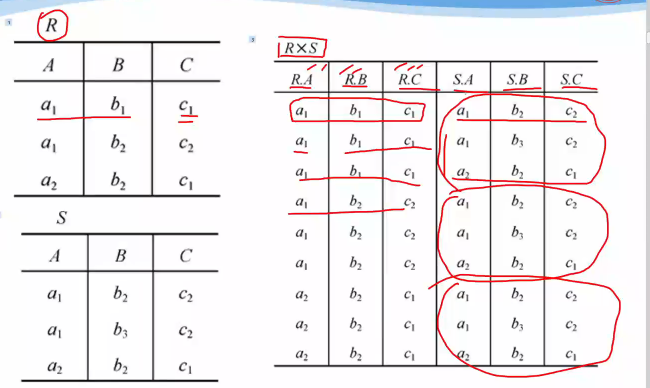






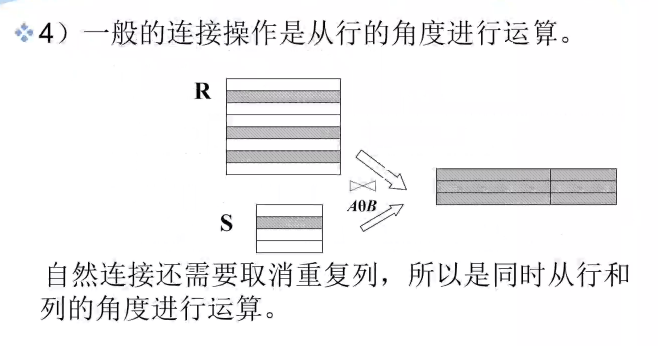
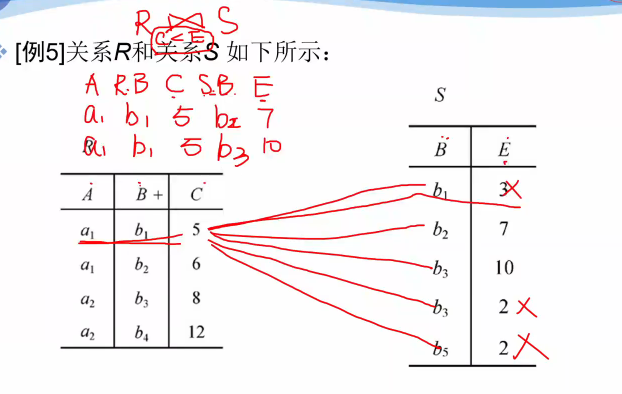
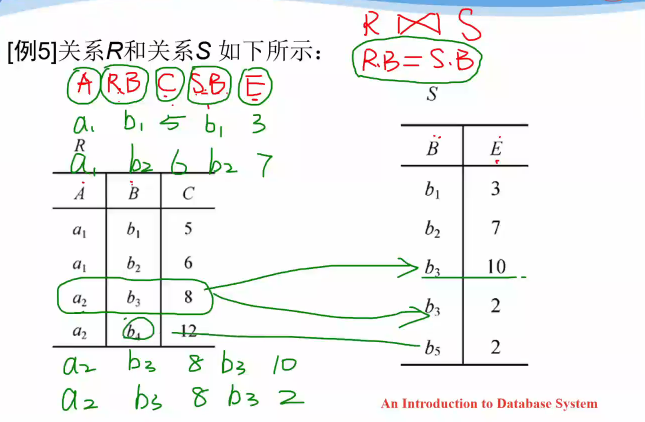
自然连接
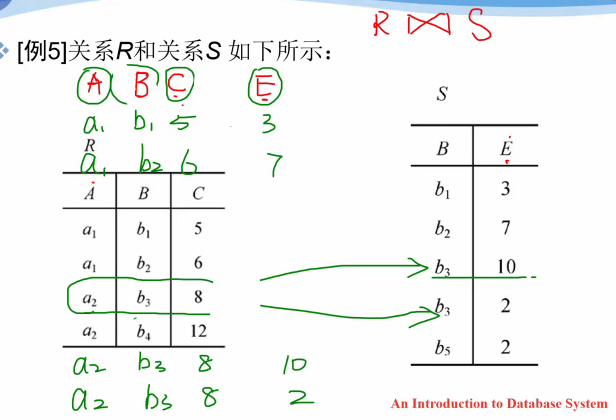




六、关系数据理论
分值最高
范式都要掌握2NF,3NF,BCNF,4NF。给你一个表,判断哪个范式
去掉部分依赖,变成2NF
去掉传递依赖,变成3NF
决定因素是码的话,就是BCNF
BCNF是去掉了主属性之间的函数传递???
